8.1. Mô hình trình tự¶
Hãy tưởng tượng rằng bạn đang xem phim trên Netflix. Là một người dùng Netflix tốt, bạn quyết định đánh giá từng bộ phim một cách tôn giáo. Rốt cuộc, một bộ phim hay là một bộ phim hay, và bạn muốn xem nhiều hơn trong số họ, phải không? Khi nó quay ra, mọi thứ không hoàn toàn đơn giản như vậy. Ý kiến của mọi người về phim có thể thay đổi khá đáng kể theo thời gian. Trên thực tế, các nhà tâm lý học thậm chí còn có tên cho một số hiệu ứng:
Có *neo *, dựa trên ý kiến của người khác. Ví dụ, sau lễ trao giải Oscar, xếp hạng cho bộ phim tương ứng tăng lên, mặc dù nó vẫn là cùng một bộ phim. Hiệu ứng này tồn tại trong vài tháng cho đến khi giải thưởng bị lãng quên. Nó đã được chỉ ra rằng hiệu ứng nâng xếp hạng lên hơn nửa điểm [Wu et al., 2017].
Có sự thích nghi * hedonic*, nơi con người nhanh chóng thích nghi để chấp nhận một tình huống cải thiện hoặc xấu đi như bình thường mới. Ví dụ, sau khi xem nhiều bộ phim hay, kỳ vọng rằng bộ phim tiếp theo cũng tốt hoặc tốt hơn là cao. Do đó, ngay cả một bộ phim trung bình cũng có thể được coi là xấu sau khi nhiều bộ phim tuyệt vời được xem.
Có * thời gian*. Rất ít người xem thích xem một bộ phim ông già Noel vào tháng 8.
Trong một số trường hợp, phim trở nên không được ưa chuộng do hành vi sai trái của đạo diễn hoặc diễn viên trong quá trình sản xuất.
Một số bộ phim trở thành phim đình đám, bởi vì chúng gần như xấu về mặt hài hước. * Plan 9 từ Outer Space* và * Troll 2* đạt được mức độ nổi tiếng cao vì lý do này.
Nói tóm lại, xếp hạng phim là bất cứ điều gì ngoài văn phòng phẩm. Do đó, sử dụng động lực thời gian đã dẫn đến các đề xuất phim chính xác hơn [Koren, 2009]. Tất nhiên, dữ liệu trình tự không chỉ là về xếp hạng phim. Sau đây cung cấp thêm hình minh họa.
Nhiều người dùng có hành vi đặc biệt cao khi nói đến thời điểm họ mở ứng dụng. Ví dụ, các ứng dụng truyền thông xã hội phổ biến hơn nhiều sau giờ học với học sinh. Các ứng dụng giao dịch thị trường chứng khoán được sử dụng phổ biến hơn khi thị trường mở cửa.
Dự đoán giá cổ phiếu ngày mai khó hơn nhiều so với việc điền vào khoảng trống cho giá cổ phiếu mà chúng tôi đã bỏ lỡ ngày hôm qua, mặc dù cả hai chỉ là vấn đề ước tính một số. Sau khi tất cả, tầm nhìn xa là khó khăn hơn nhiều so với nhận thức sau. Trong thống kê, trước đây (dự đoán vượt ra ngoài các quan sát đã biết) được gọi là * ngoại trị* trong khi sau (ước tính giữa các quan sát hiện có) được gọi là nội suy.
Âm nhạc, lời nói, văn bản và video đều có tính chất tuần tự. Nếu chúng ta hoán vị họ, họ sẽ có ý nghĩa rất ít. Tiêu đề * chó cắn người đàn ông* ít đáng ngạc nhiên hơn nhiều so với * người đàn ông cắn chó*, mặc dù các từ giống hệt nhau.
Động đất có mối tương quan mạnh mẽ, tức là, sau một trận động đất lớn, rất có thể có một số dư chấn nhỏ hơn, nhiều hơn nhiều so với không có trận động đất mạnh. Trên thực tế, động đất có tương quan về mặt không gian, tức là các dư chấn thường xảy ra trong khoảng thời gian ngắn và ở gần.
Con người tương tác với nhau trong một bản chất tuần tự, như có thể thấy trong các trận đánh Twitter, mô hình khiêu vũ và các cuộc tranh luận.
8.1.1. Công cụ thống kê¶
Chúng ta cần các công cụ thống kê và kiến trúc mạng thần kinh sâu mới để xử lý dữ liệu trình tự. Để giữ cho mọi thứ đơn giản, chúng tôi sử dụng giá cổ phiếu (chỉ số FTSE 100) được minh họa trong Fig. 8.1.1 làm ví dụ.
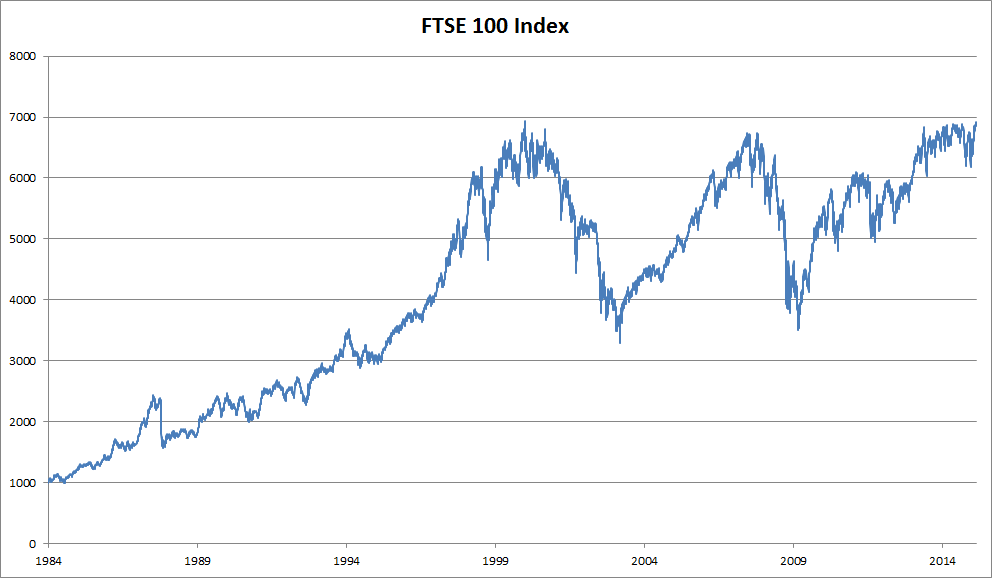
Fig. 8.1.1 FTSE 100 index over about 30 years.¶
Hãy để chúng tôi biểu thị giá bởi \(x_t\), tức là, tại bước thời gian* \(t \in \mathbb{Z}^+\) chúng tôi quan sát giá \(x_t\). Lưu ý rằng đối với chuỗi trong văn bản này, \(t\) thường sẽ rời rạc và thay đổi theo số nguyên hoặc tập con của nó. Giả sử rằng một nhà giao dịch muốn làm tốt trên thị trường chứng khoán vào ngày \(t\) dự đoán \(x_t\) qua
8.1.1.1. Mô hình Autoregressive¶
Để đạt được điều này, nhà giao dịch của chúng tôi có thể sử dụng mô hình hồi quy như mô hình mà chúng tôi đã đào tạo trong Section 3.3. Chỉ có một vấn đề lớn: số lượng đầu vào, \(x_{t-1}, \ldots, x_1\) thay đổi, tùy thuộc vào \(t\). Điều đó có nghĩa là, số lượng tăng lên theo lượng dữ liệu mà chúng ta gặp phải và chúng ta sẽ cần một xấp xỉ để làm cho tính toán này có thể truy xuất được. Phần lớn những gì sau trong chương này sẽ xoay quanh cách ước tính \(P(x_t \mid x_{t-1}, \ldots, x_1)\) hiệu quả. Tóm lại, nó có hai chiến lược như sau.
Đầu tiên, giả sử rằng chuỗi \(x_{t-1}, \ldots, x_1\) có khả năng khá dài là không thực sự cần thiết. Trong trường hợp này, chúng ta có thể tự hài lòng với một số khoảng thời gian có độ dài \(\tau\) và chỉ sử dụng các quan sát \(x_{t-1}, \ldots, x_{t-\tau}\). Lợi ích ngay lập tức là bây giờ số lượng lập luận luôn giống nhau, ít nhất là đối với \(t > \tau\). Điều này cho phép chúng tôi đào tạo một mạng sâu như đã chỉ ra ở trên. Các mô hình như vậy sẽ được gọi là mô hình * autoregressive mẫu*, vì chúng khá thực hiện hồi quy trên chính họ.
Chiến lược thứ hai, thể hiện trong Fig. 8.1.2, là giữ một số bản tóm tắt \(h_t\) của các quan sát trong quá khứ, và đồng thời cập nhật \(h_t\) ngoài dự đoán \(\hat{x}_t\). Điều này dẫn đến các mô hình ước tính \(x_t\) với \(\hat{x}_t = P(x_t \mid h_{t})\) và hơn nữa các bản cập nhật của mẫu \(h_t = g(h_{t-1}, x_{t-1})\). Vì \(h_t\) không bao giờ được quan sát, các mô hình này còn được gọi là * mô hình tự động tiềm mật*.
Fig. 8.1.2 A latent autoregressive model.¶
Cả hai trường hợp đều đặt ra câu hỏi rõ ràng về cách tạo dữ liệu đào tạo. Người ta thường sử dụng các quan sát lịch sử để dự đoán quan sát tiếp theo cho các quan sát đến ngay bây giờ. Rõ ràng chúng tôi không mong đợi thời gian để đứng yên. Tuy nhiên, một giả định phổ biến là trong khi các giá trị cụ thể của \(x_t\) có thể thay đổi, ít nhất động lực của dãy tự sẽ không. Điều này là hợp lý, vì động lực mới chỉ là thế, mới lạ và do đó không thể dự đoán được bằng cách sử dụng dữ liệu mà chúng ta có cho đến nay. Các nhà thống kê gọi động lực không thay đổi* đứng yên *. Bất kể những gì chúng tôi làm, do đó chúng tôi sẽ nhận được ước tính của toàn bộ chuỗi thông qua
Lưu ý rằng những cân nhắc trên vẫn giữ nếu chúng ta đối phó với các đối tượng rời rạc, chẳng hạn như các từ, chứ không phải là số liên tục. Sự khác biệt duy nhất là trong một tình huống như vậy chúng ta cần sử dụng một phân loại chứ không phải là một mô hình hồi quy để ước tính \(P(x_t \mid x_{t-1}, \ldots, x_1)\).
8.1.1.2. Mô hình Markov¶
Nhớ lại xấp xỉ rằng trong một mô hình autoregressive, chúng tôi chỉ sử dụng \(x_{t-1}, \ldots, x_{t-\tau}\) thay vì \(x_{t-1}, \ldots, x_1\) để ước tính \(x_t\). Bất cứ khi nào xấp xỉ này là chính xác, chúng tôi nói rằng trình tự đáp ứng một điều kiện * Markov. Đặc biệt, nếu :math:`tau = 1`, chúng tôi có mô hình Markov đơn hàng đầu tiên* và \(P(x)\) được đưa ra bởi
Các mô hình như vậy đặc biệt tốt đẹp bất cứ khi nào \(x_t\) giả định chỉ là một giá trị rời rạc, vì trong trường hợp này lập trình động có thể được sử dụng để tính toán các giá trị dọc theo chuỗi chính xác. Ví dụ, chúng ta có thể tính toán \(P(x_{t+1} \mid x_{t-1})\) một cách hiệu quả:
bằng cách sử dụng thực tế là chúng ta chỉ cần tính đến một lịch sử rất ngắn về các quan sát trong quá khứ: \(P(x_{t+1} \mid x_t, x_{t-1}) = P(x_{t+1} \mid x_t)\). Đi sâu vào chi tiết về lập trình động là vượt quá phạm vi của phần này. Kiểm soát và củng cố các thuật toán học tập sử dụng rộng rãi các công cụ như vậy.
8.1.1.3. Quan hệ nhân quả¶
Về nguyên tắc, không có gì sai khi mở ra \(P(x_1, \ldots, x_T)\) theo thứ tự ngược lại. Rốt cuộc, bằng cách điều hòa, chúng ta luôn có thể viết nó qua
Trong thực tế, nếu chúng ta có một mô hình Markov, chúng ta cũng có thể có được một phân phối xác suất có điều kiện ngược lại. Tuy nhiên, trong nhiều trường hợp, tồn tại một hướng tự nhiên cho dữ liệu, cụ thể là đi về phía trước trong thời gian. Rõ ràng là các sự kiện trong tương lai không thể ảnh hưởng đến quá khứ. Do đó, nếu chúng ta thay đổi \(x_t\), chúng ta có thể ảnh hưởng đến những gì xảy ra cho \(x_{t+1}\) trong tương lai nhưng không phải là cuộc trò chuyện. Đó là, nếu chúng ta thay đổi \(x_t\), sự phân phối trong các sự kiện trong quá khứ sẽ không thay đổi. Do đó, nó phải được dễ dàng hơn để giải thích \(P(x_{t+1} \mid x_t)\) hơn là \(P(x_t \mid x_{t+1})\). Ví dụ, nó đã được chỉ ra rằng trong một số trường hợp, chúng ta có thể tìm thấy \(x_{t+1} = f(x_t) + \epsilon\) đối với một số tiếng ồn phụ gia \(\epsilon\), trong khi cuộc trò chuyện không đúng [Hoyer et al., 2009]. Đây là một tin tuyệt vời, vì nó thường là hướng về phía trước mà chúng tôi quan tâm đến việc ước tính. Cuốn sách của Peters et al. đã giải thích thêm về chủ đề này [Peters et al., 2017a]. Chúng tôi hầu như không gãi bề mặt của nó.
8.1.2. Đào tạo¶
Sau khi xem xét rất nhiều công cụ thống kê, chúng ta hãy thử điều này trong thực tế. Chúng tôi bắt đầu bằng cách tạo ra một số dữ liệu. Để giữ cho mọi thứ đơn giản, chúng tôi tạo ra dữ liệu trình tự của chúng tôi bằng cách sử dụng một hàm sin với một số tiếng ồn phụ gia cho các bước thời gian \(1, 2, \ldots, 1000\).
%matplotlib inline
from mxnet import autograd, gluon, init, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l
npx.set_np()
T = 1000 # Generate a total of 1000 points
time = np.arange(1, T + 1, dtype=np.float32)
x = np.sin(0.01 * time) + np.random.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
T = 1000 # Generate a total of 1000 points
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))
%matplotlib inline
import tensorflow as tf
from d2l import tensorflow as d2l
T = 1000 # Generate a total of 1000 points
time = tf.range(1, T + 1, dtype=tf.float32)
x = tf.sin(0.01 * time) + tf.random.normal([T], 0, 0.2)
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))
Tiếp theo, chúng ta cần biến một chuỗi như vậy thành các tính năng và nhãn mà mô hình của chúng ta có thể đào tạo. Dựa trên kích thước nhúng \(\tau\), chúng tôi ánh xạ dữ liệu thành các cặp \(y_t = x_t\) và \(\mathbf{x}_t = [x_{t-\tau}, \ldots, x_{t-1}]\). Người đọc tinh xao có thể nhận thấy rằng điều này cho chúng ta \(\tau\) ít ví dụ dữ liệu hơn, vì chúng tôi không có đủ lịch sử cho \(\tau\) đầu tiên trong số chúng. Một sửa chữa đơn giản, đặc biệt nếu trình tự dài, là loại bỏ một vài thuật ngữ đó. Ngoài ra, chúng ta có thể pad chuỗi với số không. Ở đây chúng tôi chỉ sử dụng 600 cặp nhãn tính năng đầu tiên để đào tạo.
tau = 4
features = np.zeros((T - tau, tau))
for i in range(tau):
features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))
batch_size, n_train = 16, 600
# Only the first `n_train` examples are used for training
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
batch_size, is_train=True)
tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):
features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))
batch_size, n_train = 16, 600
# Only the first `n_train` examples are used for training
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
batch_size, is_train=True)
tau = 4
features = tf.Variable(tf.zeros((T - tau, tau)))
for i in range(tau):
features[:, i].assign(x[i: T - tau + i])
labels = tf.reshape(x[tau:], (-1, 1))
batch_size, n_train = 16, 600
# Only the first `n_train` examples are used for training
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
batch_size, is_train=True)
Ở đây chúng ta giữ kiến trúc khá đơn giản: chỉ một MLP với hai lớp được kết nối hoàn toàn, kích hoạt ReLU và tổn thất bình phương.
# A simple MLP
def get_net():
net = nn.Sequential()
net.add(nn.Dense(10, activation='relu'),
nn.Dense(1))
net.initialize(init.Xavier())
return net
# Square loss
loss = gluon.loss.L2Loss()
# Function for initializing the weights of the network
def init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
# A simple MLP
def get_net():
net = nn.Sequential(nn.Linear(4, 10),
nn.ReLU(),
nn.Linear(10, 1))
net.apply(init_weights)
return net
# Note: `MSELoss` computes squared error without the 1/2 factor
loss = nn.MSELoss(reduction='none')
# Vanilla MLP architecture
def get_net():
net = tf.keras.Sequential([tf.keras.layers.Dense(10, activation='relu'),
tf.keras.layers.Dense(1)])
return net
# Note: `MeanSquaredError` computes squared error without the 1/2 factor
loss = tf.keras.losses.MeanSquaredError()
Bây giờ chúng tôi đã sẵn sàng để đào tạo mô hình. Mã dưới đây về cơ bản là giống hệt với vòng đào tạo trong các phần trước, chẳng hạn như Section 3.3. Do đó, chúng tôi sẽ không đi sâu vào nhiều chi tiết.
def train(net, train_iter, loss, epochs, lr):
trainer = gluon.Trainer(net.collect_params(), 'adam',
{'learning_rate': lr})
for epoch in range(epochs):
for X, y in train_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
trainer.step(batch_size)
print(f'epoch {epoch + 1}, '
f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')
net = get_net()
train(net, train_iter, loss, 5, 0.01)
[10:42:56] src/base.cc:49: GPU context requested, but no GPUs found.
epoch 1, loss: 0.036144
epoch 2, loss: 0.030893
epoch 3, loss: 0.028799
epoch 4, loss: 0.028142
epoch 5, loss: 0.027056
def train(net, train_iter, loss, epochs, lr):
trainer = torch.optim.Adam(net.parameters(), lr)
for epoch in range(epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.sum().backward()
trainer.step()
print(f'epoch {epoch + 1}, '
f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')
net = get_net()
train(net, train_iter, loss, 5, 0.01)
epoch 1, loss: 0.062616
epoch 2, loss: 0.054403
epoch 3, loss: 0.054915
epoch 4, loss: 0.052986
epoch 5, loss: 0.053715
def train(net, train_iter, loss, epochs, lr):
trainer = tf.keras.optimizers.Adam()
for epoch in range(epochs):
for X, y in train_iter:
with tf.GradientTape() as g:
out = net(X)
l = loss(y, out)
params = net.trainable_variables
grads = g.gradient(l, params)
trainer.apply_gradients(zip(grads, params))
print(f'epoch {epoch + 1}, '
f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')
net = get_net()
train(net, train_iter, loss, 5, 0.01)
epoch 1, loss: 0.170327
epoch 2, loss: 0.079626
epoch 3, loss: 0.063393
epoch 4, loss: 0.061084
epoch 5, loss: 0.059050
8.1.3. Prediction¶
Vì sự mất mát đào tạo là nhỏ, chúng tôi mong đợi mô hình của chúng tôi sẽ hoạt động tốt. Hãy để chúng tôi xem điều này có nghĩa là gì trong thực tế. Điều đầu tiên cần kiểm tra là mô hình có thể dự đoán điều gì xảy ra chỉ trong bước thời gian tới, cụ thể là dự đoán * một bước trước *.
onestep_preds = net(features)
d2l.plot([time, time[tau:]], [x.asnumpy(), onestep_preds.asnumpy()], 'time',
'x', legend=['data', '1-step preds'], xlim=[1, 1000], figsize=(6, 3))
onestep_preds = net(features)
d2l.plot([time, time[tau:]], [x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
'x', legend=['data', '1-step preds'], xlim=[1, 1000], figsize=(6, 3))
onestep_preds = net(features)
d2l.plot([time, time[tau:]], [x.numpy(), onestep_preds.numpy()], 'time',
'x', legend=['data', '1-step preds'], xlim=[1, 1000], figsize=(6, 3))
Các dự đoán một bước trước trông đẹp, giống như chúng tôi mong đợi. Thậm
chí vượt quá 604 (n_train + tau) quan sát các dự đoán vẫn trông đáng
tin cậy. Tuy nhiên, chỉ có một vấn đề nhỏ đối với điều này: nếu chúng ta
chỉ quan sát dữ liệu trình tự cho đến bước thời gian 604, chúng ta không
thể hy vọng nhận được các đầu vào cho tất cả các dự đoán trước một bước
trong tương lai. Thay vào đó, chúng ta cần phải làm việc theo cách của
chúng tôi về phía trước một bước tại một thời điểm:
Nói chung, đối với một chuỗi quan sát lên đến \(x_t\), sản lượng dự đoán của nó \(\hat{x}_{t+k}\) tại bước thời điểm \(t+k\) được gọi là \(k\)* -bước trước dự đoán *. Vì chúng tôi đã quan sát đến \(x_{604}\), dự đoán \(k\)-bước trước của nó là \(\hat{x}_{604+k}\). Nói cách khác, chúng ta sẽ phải sử dụng dự đoán của riêng mình để đưa ra dự đoán nhiều bước trước. Hãy để chúng tôi xem điều này diễn ra tốt như thế nào.
multistep_preds = np.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
multistep_preds[i] = net(
multistep_preds[i - tau:i].reshape((1, -1)))
d2l.plot([time, time[tau:], time[n_train + tau:]],
[x.asnumpy(), onestep_preds.asnumpy(),
multistep_preds[n_train + tau:].asnumpy()], 'time',
'x', legend=['data', '1-step preds', 'multistep preds'],
xlim=[1, 1000], figsize=(6, 3))
multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
multistep_preds[i] = net(
multistep_preds[i - tau:i].reshape((1, -1)))
d2l.plot([time, time[tau:], time[n_train + tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy(),
multistep_preds[n_train + tau:].detach().numpy()], 'time',
'x', legend=['data', '1-step preds', 'multistep preds'],
xlim=[1, 1000], figsize=(6, 3))
multistep_preds = tf.Variable(tf.zeros(T))
multistep_preds[:n_train + tau].assign(x[:n_train + tau])
for i in range(n_train + tau, T):
multistep_preds[i].assign(tf.reshape(net(
tf.reshape(multistep_preds[i - tau: i], (1, -1))), ()))
d2l.plot([time, time[tau:], time[n_train + tau:]],
[x.numpy(), onestep_preds.numpy(),
multistep_preds[n_train + tau:].numpy()], 'time',
'x', legend=['data', '1-step preds', 'multistep preds'],
xlim=[1, 1000], figsize=(6, 3))
Như ví dụ trên cho thấy, đây là một thất bại ngoạn mục. Các dự đoán phân rã thành một hằng số khá nhanh sau một vài bước dự đoán. Tại sao thuật toán hoạt động rất kém? Điều này cuối cùng là do thực tế là các lỗi xây dựng. Chúng ta hãy nói rằng sau bước 1 chúng ta có một số lỗi \(\epsilon_1 = \bar\epsilon\). Bây giờ đầu vào cho bước 2 bị ảnh hưởng bởi \(\epsilon_1\), do đó chúng tôi bị một số lỗi theo thứ tự \(\epsilon_2 = \bar\epsilon + c \epsilon_1\) đối với một số hằng số \(c\), v.v. Lỗi có thể phân kỳ khá nhanh từ các quan sát thực sự. Đây là một hiện tượng phổ biến. Ví dụ, dự báo thời tiết trong 24 giờ tới có xu hướng khá chính xác nhưng ngoài đó độ chính xác giảm nhanh chóng. Chúng tôi sẽ thảo luận về các phương pháp để cải thiện điều này trong suốt chương này và hơn thế nữa.
Hãy để chúng tôi xem xét kỹ hơn những khó khăn trong \(k\)-bước trước dự đoán bằng cách tính toán dự đoán trên toàn bộ chuỗi cho \(k = 1, 4, 16, 64\).
max_steps = 64
features = np.zeros((T - tau - max_steps + 1, tau + max_steps))
# Column `i` (`i` < `tau`) are observations from `x` for time steps from
# `i + 1` to `i + T - tau - max_steps + 1`
for i in range(tau):
features[:, i] = x[i: i + T - tau - max_steps + 1]
# Column `i` (`i` >= `tau`) are the (`i - tau + 1`)-step-ahead predictions for
# time steps from `i + 1` to `i + T - tau - max_steps + 1`
for i in range(tau, tau + max_steps):
features[:, i] = net(features[:, i - tau:i]).reshape(-1)
steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
[features[:, (tau + i - 1)].asnumpy() for i in steps], 'time', 'x',
legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
figsize=(6, 3))
max_steps = 64
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
# Column `i` (`i` < `tau`) are observations from `x` for time steps from
# `i + 1` to `i + T - tau - max_steps + 1`
for i in range(tau):
features[:, i] = x[i: i + T - tau - max_steps + 1]
# Column `i` (`i` >= `tau`) are the (`i - tau + 1`)-step-ahead predictions for
# time steps from `i + 1` to `i + T - tau - max_steps + 1`
for i in range(tau, tau + max_steps):
features[:, i] = net(features[:, i - tau:i]).reshape(-1)
steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
[features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
figsize=(6, 3))
max_steps = 64
features = tf.Variable(tf.zeros((T - tau - max_steps + 1, tau + max_steps)))
# Column `i` (`i` < `tau`) are observations from `x` for time steps from
# `i + 1` to `i + T - tau - max_steps + 1`
for i in range(tau):
features[:, i].assign(x[i: i + T - tau - max_steps + 1].numpy())
# Column `i` (`i` >= `tau`) are the (`i - tau + 1`)-step-ahead predictions for
# time steps from `i + 1` to `i + T - tau - max_steps + 1`
for i in range(tau, tau + max_steps):
features[:, i].assign(tf.reshape(net((features[:, i - tau: i])), -1))
steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
[features[:, (tau + i - 1)].numpy() for i in steps], 'time', 'x',
legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
figsize=(6, 3))
Điều này minh họa rõ ràng chất lượng dự đoán thay đổi như thế nào khi chúng ta cố gắng dự đoán thêm vào tương lai. Trong khi các dự đoán 4 bước trước vẫn trông tốt, nhưng bất cứ điều gì ngoài đó là gần như vô dụng.
8.1.4. Tóm tắt¶
Có khá một sự khác biệt về khó khăn giữa nội suy và ngoại suy. Do đó, nếu bạn có một chuỗi, hãy luôn tôn trọng thứ tự thời gian của dữ liệu khi đào tạo, tức là, không bao giờ đào tạo về dữ liệu trong tương lai.
Các mô hình trình tự yêu cầu các công cụ thống kê chuyên dụng để ước tính. Hai lựa chọn phổ biến là mô hình autoregressive và các mô hình autoregressive biến trễ.
Đối với các mô hình nhân quả (ví dụ: thời gian đi về phía trước), ước tính hướng tiến thường dễ dàng hơn rất nhiều so với hướng ngược lại.
Đối với một chuỗi quan sát đến thời gian bước \(t\), đầu ra dự đoán của nó tại bước thời gian \(t+k\) là \(k\)* -bước trước dự đoán *. Như chúng ta dự đoán thêm trong thời gian bằng cách tăng \(k\), các lỗi tích lũy và chất lượng dự đoán suy giảm, thường đáng kể.
8.1.5. Bài tập¶
Cải thiện mô hình trong thí nghiệm của phần này.
Kết hợp nhiều hơn 4 quan sát trong quá khứ? Bạn thực sự cần bao nhiêu?
Bạn sẽ cần bao nhiêu quan sát trong quá khứ nếu không có tiếng ồn? Gợi ý: bạn có thể viết \(\sin\) và \(\cos\) dưới dạng phương trình vi phân.
Bạn có thể kết hợp các quan sát cũ hơn trong khi vẫn giữ tổng số tính năng không đổi? Điều này có cải thiện độ chính xác không? Tại sao?
Thay đổi kiến trúc mạng thần kinh và đánh giá hiệu suất.
Một nhà đầu tư muốn tìm một bảo mật tốt để mua. Anh ta nhìn vào sự trở lại trong quá khứ để quyết định cái nào có khả năng làm tốt. Điều gì có thể xảy ra sai với chiến lược này?
Liệu nhân quả cũng áp dụng cho văn bản? Đến mức nào?
Đưa ra một ví dụ cho khi một mô hình tự hồi quy tiềm ẩn có thể cần thiết để nắm bắt động của dữ liệu.
