4.9. Môi trường và phân phối Shift¶
Trong các phần trước, chúng tôi đã làm việc thông qua một số ứng dụng thực hành của machine learning, phù hợp với các mô hình cho nhiều bộ dữ liệu khác nhau. Tuy nhiên, chúng tôi không bao giờ dừng lại để chiêm ngưỡng dữ liệu đến từ đâu ở nơi đầu tiên hoặc những gì chúng tôi dự định cuối cùng làm với các đầu ra từ các mô hình của chúng tôi. Quá thường xuyên, các nhà phát triển machine learning sở hữu dữ liệu vội vàng phát triển các mô hình mà không dừng lại để xem xét những vấn đề cơ bản này.
Nhiều triển khai machine learning thất bại có thể được truy trở lại mô hình này. Đôi khi các mô hình dường như thực hiện tuyệt vời như được đo bằng độ chính xác của bộ thử nghiệm nhưng thất bại thảm khốc trong việc triển khai khi phân phối dữ liệu đột ngột thay đổi. Ngấm ngầm hơn, đôi khi việc triển khai một mô hình có thể là chất xúc tác làm xáo trộn phân phối dữ liệu. Ví dụ, ví dụ, chúng tôi đã đào tạo một mô hình để dự đoán ai sẽ trả nợ so với mặc định cho vay, thấy rằng lựa chọn giày dép của người nộp đơn có liên quan đến rủi ro mặc định (Oxfords cho biết trả nợ, giày thể thao chỉ ra mặc định). Sau đó chúng tôi có thể có xu hướng cấp các khoản vay cho tất cả các ứng viên mặc Oxfords và từ chối tất cả các ứng viên mang giày thể thao.
Trong trường hợp này, bước nhảy vọt không được coi là của chúng tôi từ công nhận mô hình đến ra quyết định và việc chúng tôi không xem xét nghiêm túc môi trường có thể có hậu quả tai hại. Để bắt đầu, ngay khi chúng tôi bắt đầu đưa ra quyết định dựa trên giày dép, khách hàng sẽ bắt kịp và thay đổi hành vi của họ. Trước lâu, tất cả các ứng viên sẽ mặc Oxfords, mà không có bất kỳ sự cải thiện trùng hợp nào về giá trị tín dụng. Dành một phút để tiêu hóa điều này bởi vì các vấn đề tương tự rất nhiều trong nhiều ứng dụng học máy: bằng cách giới thiệu các quyết định dựa trên mô hình của chúng tôi cho môi trường, chúng tôi có thể phá vỡ mô hình.
Mặc dù chúng tôi không thể cung cấp cho các chủ đề này một phương pháp điều trị hoàn chỉnh trong một phần, chúng tôi đặt mục tiêu ở đây để phơi bày một số mối quan tâm phổ biến và kích thích tư duy phê phán cần thiết để phát hiện sớm những tình huống này, giảm thiểu thiệt hại và sử dụng máy học một cách có trách nhiệm. Một số giải pháp rất đơn giản (yêu cầu dữ liệu “đúng”), một số là khó khăn về mặt kỹ thuật (thực hiện một hệ thống học tập tăng cường), và những người khác yêu cầu chúng ta bước ra ngoài lĩnh vực dự đoán thống kê hoàn toàn và vật lộn với các câu hỏi triết học khó liên quan đến ứng dụng đạo đức của algorithms thuật toán.
4.9.1. Các loại dịch chuyển phân phối¶
Để bắt đầu, chúng tôi gắn bó với cài đặt dự đoán thụ động xem xét các cách khác nhau mà các phân phối dữ liệu có thể thay đổi và những gì có thể được thực hiện để cứu vớt hiệu suất mô hình. Trong một thiết lập cổ điển, chúng tôi giả định rằng dữ liệu đào tạo của chúng tôi đã được lấy mẫu từ một số phân phối \(p_S(\mathbf{x},y)\) nhưng dữ liệu thử nghiệm của chúng tôi sẽ bao gồm các ví dụ không có nhãn được rút ra từ một số phân phối khác nhau \(p_T(\mathbf{x},y)\). Đã, chúng ta phải đối đầu với một thực tế tỉnh táo. Vắng mặt bất kỳ giả định nào về cách \(p_S\) và \(p_T\) liên quan đến nhau, việc học một bộ phân loại mạnh mẽ là không thể.
Hãy xem xét một vấn đề phân loại nhị phân, nơi chúng ta muốn phân biệt giữa chó và mèo. Nếu phân phối có thể thay đổi theo những cách tùy ý, thì thiết lập của chúng tôi cho phép trường hợp bệnh lý trong đó phân phối trên đầu vào vẫn không đổi: \(p_S(\mathbf{x}) = p_T(\mathbf{x})\), nhưng các nhãn đều bị lật: \(p_S(y | \mathbf{x}) = 1 - p_T(y | \mathbf{x})\). Nói cách khác, nếu Thiên Chúa đột nhiên có thể quyết định rằng trong tương lai tất cả các “mèo” bây giờ là chó và những gì trước đây chúng ta gọi là “chó” bây giờ là mèo - mà không có bất kỳ thay đổi nào trong phân phối đầu vào \(p(\mathbf{x})\), thì chúng ta không thể phân biệt được cài đặt này với một trong đó phân phối không thay đổi chút nào.
May mắn thay, dưới một số giả định bị hạn chế về cách dữ liệu của chúng ta có thể thay đổi trong tương lai, các thuật toán nguyên tắc có thể phát hiện sự thay đổi và đôi khi thậm chí thích ứng ngay lập tức, cải thiện độ chính xác của phân loại ban đầu.
4.9.1.1. Covariate Shift¶
Trong số các loại dịch chuyển phân phối, sự thay đổi đồng biến có thể được nghiên cứu rộng rãi nhất. Ở đây, chúng tôi giả định rằng trong khi phân phối các đầu vào có thể thay đổi theo thời gian, chức năng ghi nhãn, tức là phân phối có điều kiện \(P(y \mid \mathbf{x})\) không thay đổi. Các nhà thống kê gọi đây là * covariate shift* vì vấn đề phát sinh do sự thay đổi trong sự phân bố của các covariates (tính năng). Mặc dù đôi khi chúng ta có thể lý do về sự thay đổi phân phối mà không gọi nhân quả, chúng tôi lưu ý rằng sự thay đổi đồng biến là giả định tự nhiên để gọi trong các cài đặt mà chúng tôi tin rằng \(\mathbf{x}\) gây ra \(y\).
Hãy xem xét thách thức phân biệt mèo và chó. Dữ liệu đào tạo của chúng tôi có thể bao gồm các hình ảnh thuộc loại trong Fig. 4.9.1.
Fig. 4.9.1 Training data for distinguishing cats and dogs.¶
Tại thời điểm thử nghiệm, chúng tôi được yêu cầu phân loại hình ảnh trong Fig. 4.9.2.
Fig. 4.9.2 Test data for distinguishing cats and dogs.¶
Bộ đào tạo bao gồm các bức ảnh, trong khi bộ thử nghiệm chỉ chứa phim hoạt hình. Đào tạo về một tập dữ liệu với các đặc điểm khác biệt đáng kể so với bộ thử nghiệm có thể đánh vần rắc rối vắng mặt một kế hoạch mạch lạc về cách thích ứng với tên miền mới.
4.9.1.2. Thay đổi nhãn¶
Label shift mô tả vấn đề converse. Ở đây, chúng tôi giả định rằng nhãn biên \(P(y)\) có thể thay đổi nhưng phân phối lớp có điều kiện \(P(\mathbf{x} \mid y)\) vẫn cố định trên các miền. Sự thay đổi nhãn là một giả định hợp lý để đưa ra khi chúng tôi tin rằng \(y\) gây ra \(\mathbf{x}\). Ví dụ, chúng tôi có thể muốn dự đoán chẩn đoán cho các triệu chứng của họ (hoặc các biểu hiện khác), ngay cả khi tỷ lệ tương đối của chẩn đoán đang thay đổi theo thời gian. Thay đổi nhãn là giả định thích hợp ở đây vì bệnh gây ra các triệu chứng. Trong một số trường hợp thoái hóa, sự dịch chuyển nhãn và các giả định thay đổi thay đổi có thể giữ đồng thời. Ví dụ, khi nhãn là xác định, giả định thay đổi đồng biến sẽ được thỏa mãn, ngay cả khi \(y\) gây ra \(\mathbf{x}\). Thật thú vị, trong những trường hợp này, nó thường thuận lợi để làm việc với các phương pháp chảy từ giả định thay đổi nhãn. Đó là bởi vì các phương pháp này có xu hướng liên quan đến việc thao tác các đối tượng trông giống như nhãn (thường là chiều thấp), trái ngược với các đối tượng trông giống như đầu vào, có xu hướng có chiều cao trong học sâu.
4.9.1.3. Concept Shift¶
Chúng tôi cũng có thể gặp phải vấn đề liên quan của concept shift, phát sinh khi các định nghĩa của nhãn có thể thay đổi. Điều này nghe có vẻ kỳ quặc một * cat* là một * cat*, không? Tuy nhiên, các danh mục khác có thể thay đổi sử dụng theo thời gian. Tiêu chí chẩn đoán cho bệnh tâm thần, những gì trôi qua cho thời trang và chức danh công việc, tất cả đều phải chịu một lượng đáng kể sự thay đổi khái niệm. Hóa ra nếu chúng ta điều hướng khắp Hoa Kỳ, chuyển nguồn dữ liệu của chúng ta theo địa lý, chúng ta sẽ tìm thấy sự thay đổi khái niệm đáng kể liên quan đến việc phân phối tên cho * đồ uống mềm* như thể hiện trong Fig. 4.9.3.
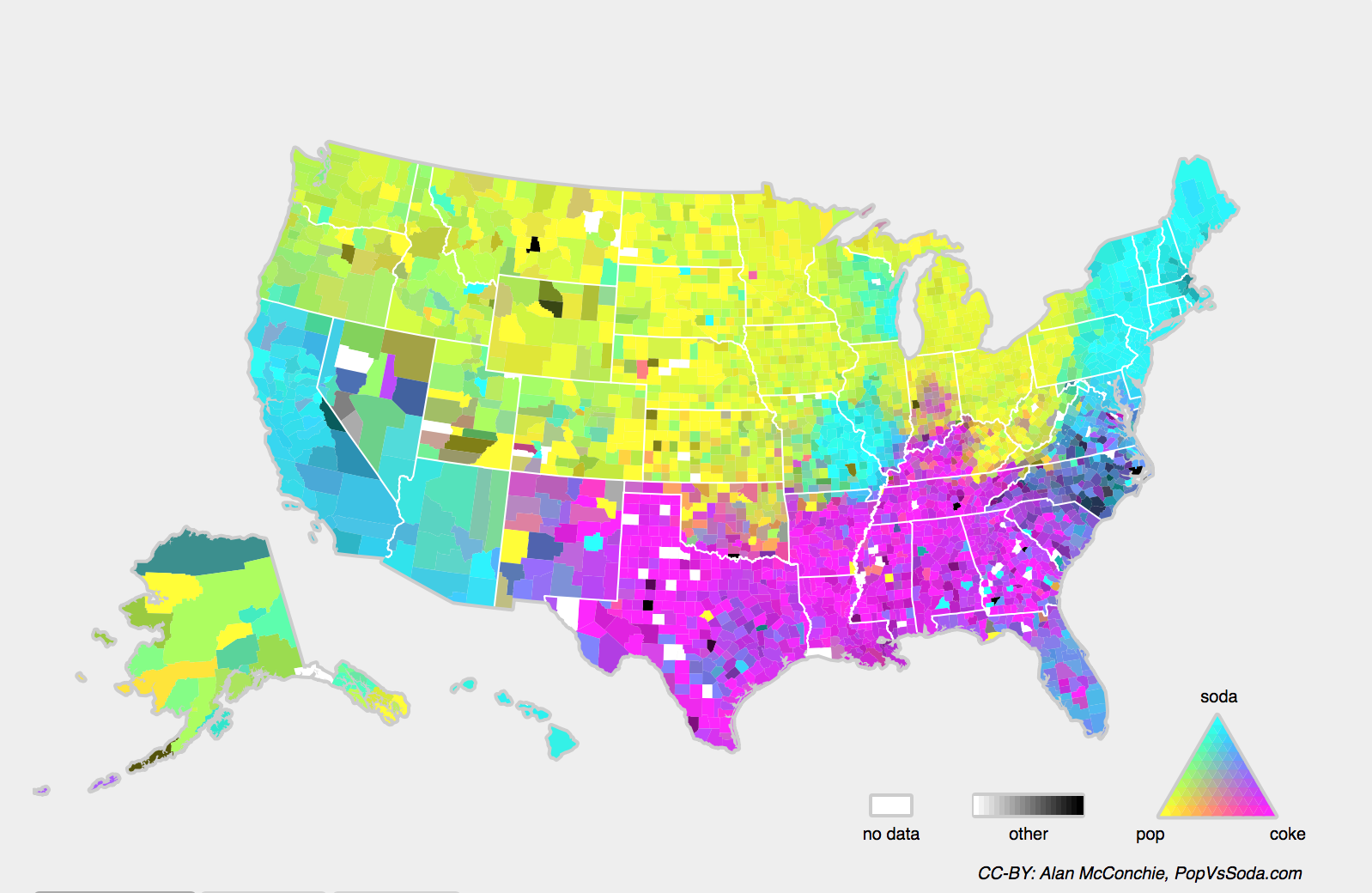
Fig. 4.9.3 Concept shift on soft drink names in the United States.¶
Nếu chúng ta xây dựng một hệ thống dịch máy, phân phối \(P(y \mid \mathbf{x})\) có thể khác nhau tùy thuộc vào vị trí của chúng tôi. Vấn đề này có thể khó phát hiện. Chúng ta có thể hy vọng sẽ khai thác kiến thức rằng sự thay đổi chỉ diễn ra dần dần theo nghĩa thời gian hoặc địa lý.
4.9.2. Ví dụ về Distribution Shift¶
Trước khi đi sâu vào chủ nghĩa hình thức và thuật toán, chúng ta có thể thảo luận về một số tình huống cụ thể mà sự thay đổi chung hoặc khái niệm có thể không rõ ràng.
4.9.2.1. Chẩn đoán y tế¶
Hãy tưởng tượng rằng bạn muốn thiết kế một thuật toán để phát hiện ung thư. Bạn thu thập dữ liệu từ những người khỏe mạnh và bệnh tật và bạn đào tạo thuật toán của mình. Nó hoạt động tốt, mang lại cho bạn độ chính xác cao và bạn kết luận rằng bạn đã sẵn sàng cho một sự nghiệp thành công trong chẩn đoán y tế. *Không quá nhanh. *
Các bản phân phối đã tạo ra dữ liệu đào tạo và những người bạn sẽ gặp phải trong tự nhiên có thể khác nhau đáng kể. Điều này đã xảy ra với một công ty khởi nghiệp đáng tiếc mà một số người trong chúng ta (tác giả) đã làm việc với nhiều năm trước. Họ đang phát triển xét nghiệm máu cho một căn bệnh chủ yếu ảnh hưởng đến những người đàn ông lớn tuổi và hy vọng nghiên cứu nó bằng cách sử dụng các mẫu máu mà họ đã thu thập từ bệnh nhân. Tuy nhiên, việc lấy mẫu máu từ những người đàn ông khỏe mạnh là khó khăn hơn đáng kể so với bệnh nhân bị bệnh đã có trong hệ thống. Để bù đắp, công ty khởi nghiệp đã yêu cầu quyên góp máu từ các sinh viên trong khuôn viên trường đại học để đóng vai trò là biện pháp kiểm soát lành mạnh trong việc phát triển bài kiểm tra của họ. Sau đó, họ hỏi liệu chúng tôi có thể giúp họ xây dựng một phân loại để phát hiện bệnh.
Như chúng tôi đã giải thích cho họ, thực sự sẽ dễ dàng phân biệt giữa các nhóm khỏe mạnh và bệnh tật với độ chính xác gần như hoàn hảo. Tuy nhiên, đó là do các đối tượng xét nghiệm khác nhau về độ tuổi, mức độ hormone, hoạt động thể chất, chế độ ăn uống, tiêu thụ rượu và nhiều yếu tố khác không liên quan đến bệnh. Điều này không có khả năng là trường hợp với bệnh nhân thực sự. Do quy trình lấy mẫu của họ, chúng ta có thể mong đợi sẽ gặp phải sự thay đổi đồng biến cực đoan. Hơn nữa, trường hợp này không có khả năng sửa chữa thông qua các phương pháp thông thường. Nói tóm lại, họ đã lãng phí một khoản tiền đáng kể.
4.9.2.2. Ô tô tự lái¶
Nói rằng một công ty muốn tận dụng máy học để phát triển những chiếc xe tự lái. Một thành phần quan trọng ở đây là một máy dò bên đường. Vì dữ liệu chú thích thực sự rất tốn kém để có được, họ đã có ý tưởng (thông minh và có vấn đề) để sử dụng dữ liệu tổng hợp từ một công cụ kết xuất trò chơi làm dữ liệu đào tạo bổ sung. Điều này hoạt động thực sự tốt trên “dữ liệu thử nghiệm” được rút ra từ công cụ kết xuất. Than ôi, bên trong một chiếc xe thực sự đó là một thảm họa. Khi nó bật ra, lề đường đã được kết xuất với một kết cấu rất đơn giản. Quan trọng hơn, * tất cả* bên lề đường đã được kết xuất với kết cấu * same* và máy dò bên đường đã tìm hiểu về “tính năng” này rất nhanh chóng.
Một điều tương tự cũng xảy ra với Quân đội Mỹ khi lần đầu tiên họ cố gắng phát hiện xe tăng trong rừng. Họ chụp những bức ảnh trên không của khu rừng không có xe tăng, sau đó lái xe tăng vào rừng và chụp một bộ ảnh khác. Bộ phân loại dường như hoạt động * hoàn hảo*. Thật không may, nó chỉ học cách phân biệt cây có bóng với cây không có bóng - bộ ảnh đầu tiên được chụp vào sáng sớm, bộ thứ hai vào buổi trưa.
4.9.2.3. Phân phối Nonstationary¶
Một tình huống tinh tế hơn nhiều phát sinh khi phân phối thay đổi chậm (còn được gọi là phân phối không cố định *) và mô hình không được cập nhật đầy đủ. Dưới đây là một số trường hợp điển hình.
Chúng tôi đào tạo một mô hình quảng cáo tính toán và sau đó không cập nhật nó thường xuyên (ví dụ: chúng tôi quên kết hợp rằng một thiết bị mới tối nghĩa gọi là iPad vừa được khởi chạy).
Chúng tôi xây dựng một bộ lọc thư rác. Nó hoạt động tốt trong việc phát hiện tất cả thư rác mà chúng ta đã thấy cho đến nay. Nhưng sau đó những kẻ gửi thư rác wisen lên và tạo ra những tin nhắn mới trông không giống như bất cứ điều gì chúng ta đã thấy trước đây.
Chúng tôi xây dựng một hệ thống khuyến nghị sản phẩm. Nó hoạt động trong suốt mùa đông nhưng sau đó tiếp tục giới thiệu mũ ông già Noel từ lâu sau Giáng sinh.
4.9.2.4. Thêm giai thoại¶
Chúng tôi xây dựng một máy dò khuôn mặt. Nó hoạt động tốt trên tất cả các điểm chuẩn. Thật không may, nó thất bại trên dữ liệu thử nghiệm - các ví dụ vi phạm là cận cảnh trong đó khuôn mặt lấp đầy toàn bộ hình ảnh (không có dữ liệu như vậy trong bộ đào tạo).
Chúng tôi xây dựng một công cụ tìm kiếm Web cho thị trường Mỹ và muốn triển khai nó ở Anh.
Chúng tôi đào tạo một bộ phân loại hình ảnh bằng cách biên dịch một tập dữ liệu lớn trong đó mỗi tập hợp lớn các lớp được biểu diễn như nhau trong tập dữ liệu, giả sử 1000 danh mục, được đại diện bởi 1000 hình ảnh mỗi. Sau đó, chúng tôi triển khai hệ thống trong thế giới thực, nơi phân phối nhãn thực tế của ảnh là quyết định không đồng nhất.
4.9.3. Sửa đổi sự thay đổi phân phối¶
Như chúng ta đã thảo luận, có nhiều trường hợp đào tạo và phân phối thử nghiệm \(P(\mathbf{x}, y)\) khác nhau. Trong một số trường hợp, chúng tôi nhận được may mắn và các mô hình hoạt động mặc dù covariate, nhãn, hoặc thay đổi khái niệm. Trong các trường hợp khác, chúng ta có thể làm tốt hơn bằng cách sử dụng các chiến lược nguyên tắc để đối phó với sự thay đổi. Phần còn lại của phần này phát triển kỹ thuật hơn đáng kể. Người đọc thiếu kiên nhẫn có thể tiếp tục đến phần tiếp theo vì tài liệu này không phải là điều kiện tiên quyết cho các khái niệm tiếp theo.
4.9.3.1. Rủi ro và rủi ro thực nghiệm¶
Trước tiên chúng ta hãy phản ánh về những gì chính xác đang xảy ra trong quá trình đào tạo mô hình: chúng tôi lặp lại các tính năng và nhãn liên quan của dữ liệu đào tạo \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\) và cập nhật các thông số của một mô hình \(f\) sau mỗi minibatch. Để đơn giản, chúng tôi không xem xét chính quy hóa, vì vậy chúng tôi phần lớn giảm thiểu sự mất mát trong đào tạo:
trong đó \(l\) là chức năng mất đo “xấu như thế nào” dự đoán \(f(\mathbf{x}_i)\) được đưa ra nhãn liên quan \(y_i\). Các nhà thống kê gọi thuật ngữ này trong (4.9.1) * rủi ro thực tế*. Rủi ro thực nghiệm * là tổn thất trung bình so với dữ liệu đào tạo để xấp xỉ * rủi ro*, đó là kỳ vọng về sự mất mát đối với toàn bộ dân số dữ liệu được rút ra từ phân phối thực sự của họ \(p(\mathbf{x},y)\):
Tuy nhiên, trong thực tế, chúng ta thường không thể có được toàn bộ dân số dữ liệu. Do đó, *giảm thiểu rủi ro thực nghiệm *, đang giảm thiểu rủi ro thực nghiệm trong (4.9.1), là một chiến lược thực tế cho việc học máy, với hy vọng sẽ giảm thiểu rủi ro gần đúng.
4.9.3.2. Covariate Shift Correction¶
Giả sử rằng chúng tôi muốn ước tính một số phụ thuộc \(P(y \mid \mathbf{x})\) mà chúng tôi đã dán nhãn dữ liệu \((\mathbf{x}_i, y_i)\). Thật không may, các quan sát \(\mathbf{x}_i\) được rút ra từ một số phân phối nguồn *\(q(\mathbf{x})\) thay vì phân phối mục tiêu *\(p(\mathbf{x})\). May mắn thay, giả định phụ thuộc có nghĩa là phân phối có điều kiện không thay đổi: \(p(y \mid \mathbf{x}) = q(y \mid \mathbf{x})\). Nếu phân phối nguồn \(q(\mathbf{x})\) là “sai”, chúng ta có thể sửa chữa điều đó bằng cách sử dụng danh tính đơn giản sau đây trong rủi ro:
Nói cách khác, chúng ta cần cân nhắc lại từng ví dụ dữ liệu theo tỷ lệ xác suất mà nó sẽ được rút ra từ phân phối chính xác đến đó từ sai:
Cắm trọng lượng \(\beta_i\) cho mỗi ví dụ dữ liệu \((\mathbf{x}_i, y_i)\) chúng ta có thể đào tạo mô hình của mình bằng cách sử dụng giảm thiểu rủi ro thực nghiệm có trọng lự:
Than ôi, chúng ta không biết tỷ lệ đó, vì vậy trước khi chúng ta có thể làm bất cứ điều gì hữu ích, chúng ta cần ước tính nó. Nhiều phương pháp có sẵn, bao gồm một số cách tiếp cận lý thuyết vận hành ưa thích mà cố gắng tái hiệu chỉnh lại toán tử kỳ vọng trực tiếp bằng cách sử dụng một tiêu chuẩn tối thiểu hoặc một nguyên tắc entropy tối đa. Lưu ý rằng đối với bất kỳ cách tiếp cận nào như vậy, chúng ta cần các mẫu được rút ra từ cả hai bản phân phối - \(p\) “đúng”, ví dụ, bằng cách truy cập vào dữ liệu thử nghiệm và mẫu được sử dụng để tạo bộ đào tạo \(q\) (sau này có sẵn tầm thường). Tuy nhiên, lưu ý rằng chúng tôi chỉ cần các tính năng \(\mathbf{x} \sim p(\mathbf{x})\); chúng tôi không cần phải truy cập nhãn \(y \sim p(y)\).
Trong trường hợp này, tồn tại một cách tiếp cận rất hiệu quả sẽ cho kết quả gần như tốt như bản gốc: hồi quy hậu cần, đó là một trường hợp đặc biệt của hồi quy softmax (xem Section 3.4) để phân loại nhị phân. Đây là tất cả những gì cần thiết để tính toán tỷ lệ xác suất ước tính. Chúng tôi học một phân loại để phân biệt giữa dữ liệu được rút ra từ \(p(\mathbf{x})\) và dữ liệu được rút ra từ \(q(\mathbf{x})\). Nếu không thể phân biệt giữa hai bản phân phối thì điều đó có nghĩa là các trường hợp liên quan đều có khả năng đến từ một trong hai bản phân phối. Mặt khác, bất kỳ trường hợp nào có thể bị phân biệt đối xử tốt nên bị quá trọng lượng hoặc giảm cân đáng kể cho phù hợp.
Vì lợi ích của đơn giản giả định rằng chúng ta có một số lượng tương đương của các phiên bản từ cả hai bản phân phối \(p(\mathbf{x})\) và \(q(\mathbf{x})\), tương ứng. Bây giờ biểu thị bằng \(z\) nhãn là \(1\) cho dữ liệu được rút ra từ \(p\) và \(-1\) cho dữ liệu được rút ra từ \(q\). Sau đó, xác suất trong một tập dữ liệu hỗn hợp được đưa ra bởi
Do đó, nếu chúng ta sử dụng phương pháp hồi quy logistic, trong đó \(P(z=1 \mid \mathbf{x})=\frac{1}{1+\exp(-h(\mathbf{x}))}\) (\(h\) là một hàm tham số hóa), nó theo sau đó
Kết quả là, chúng ta cần giải quyết hai vấn đề: đầu tiên là phân biệt giữa dữ liệu được rút ra từ cả hai bản phân phối, và sau đó là một vấn đề giảm thiểu rủi ro theo kinh nghiệm có trọng số trong (4.9.5), nơi chúng ta cân nhắc các thuật ngữ \(\beta_i\).
Bây giờ chúng tôi đã sẵn sàng để mô tả một thuật toán hiệu chỉnh. Giả sử rằng chúng tôi có một bộ đào tạo \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\) và một bộ thử nghiệm không có nhãn \(\{\mathbf{u}_1, \ldots, \mathbf{u}_m\}\). Đối với sự thay đổi hợp phương, chúng tôi giả định rằng \(\mathbf{x}_i\) cho tất cả \(1 \leq i \leq n\) được rút ra từ một số phân phối nguồn và \(\mathbf{u}_i\) cho tất cả \(1 \leq i \leq m\) được rút ra từ phân phối mục tiêu. Dưới đây là một thuật toán nguyên mẫu để sửa đổi dịch chuyển đồng biến:
Tạo một bộ đào tạo phân loại nhị phân: \(\{(\mathbf{x}_1, -1), \ldots, (\mathbf{x}_n, -1), (\mathbf{u}_1, 1), \ldots, (\mathbf{u}_m, 1)\}\).
Đào tạo một phân loại nhị phân sử dụng hồi quy logistic để có được chức năng \(h\).
Cân dữ liệu đào tạo sử dụng \(\beta_i = \exp(h(\mathbf{x}_i))\) hoặc tốt hơn \(\beta_i = \min(\exp(h(\mathbf{x}_i)), c)\) cho một số hằng số \(c\).
Sử dụng trọng lượng \(\beta_i\) để đào tạo trên \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\) trong (4.9.5).
Lưu ý rằng thuật toán trên dựa vào một giả định quan trọng. Để chương trình này hoạt động, chúng ta cần rằng mỗi ví dụ dữ liệu trong phân phối mục tiêu (ví dụ: thời gian thử nghiệm) có xác suất không xảy ra tại thời điểm đào tạo. Nếu chúng ta tìm thấy một điểm mà \(p(\mathbf{x}) > 0\) nhưng \(q(\mathbf{x}) = 0\), thì trọng lượng tầm quan trọng tương ứng nên là vô cùng.
4.9.3.3. Hiệu chỉnh thay đổi nhãn¶
Giả sử rằng chúng tôi đang đối phó với một nhiệm vụ phân loại với \(k\) loại. Sử dụng cùng một ký hiệu trong Section 4.9.3.2, \(q\) và \(p\) là phân phối nguồn (ví dụ, thời gian đào tạo) và phân phối mục tiêu (ví dụ, thời gian thử nghiệm), tương ứng. Giả sử rằng việc phân phối nhãn thay đổi theo thời gian: \(q(y) \neq p(y)\), nhưng phân phối lớp có điều kiện vẫn giữ nguyên: \(q(\mathbf{x} \mid y)=p(\mathbf{x} \mid y)\). Nếu phân phối nguồn \(q(y)\) là “sai”, chúng ta có thể sửa chữa điều đó theo danh tính sau trong rủi ro như được định nghĩa trong (4.9.2):
Ở đây, trọng lượng tầm quan trọng của chúng tôi sẽ tương ứng với tỷ lệ khả năng nhãn
Một điều hay về sự thay đổi nhãn là nếu chúng ta có một mô hình hợp lý tốt về phân phối nguồn, thì chúng ta có thể nhận được ước tính nhất quán về các trọng lượng này mà không cần phải đối phó với kích thước xung quanh. Trong học sâu, các đầu vào có xu hướng là các đối tượng có chiều cao như hình ảnh, trong khi nhãn thường là các đối tượng đơn giản hơn như các danh mục.
Để ước tính phân phối nhãn mục tiêu, trước tiên chúng tôi lấy bộ phân loại ngoài giá trị hợp lý của chúng tôi (thường được đào tạo về dữ liệu đào tạo) và tính toán ma trận nhầm lẫn của nó bằng cách sử dụng bộ xác thực (cũng từ phân phối đào tạo). Ma trận nhầm lúc, \(\mathbf{C}\), chỉ đơn giản là ma trận \(k \times k\), trong đó mỗi cột tương ứng với danh mục nhãn (sự thật mặt đất) và mỗi hàng tương ứng với danh mục dự đoán của mô hình của chúng tôi. Giá trị của mỗi ô \(c_{ij}\) là một phần của tổng dự đoán trên bộ xác thực trong đó nhãn thực là \(j\) và mô hình của chúng tôi dự đoán \(i\).
Bây giờ, chúng ta không thể tính toán ma trận nhầm lẫn trên dữ liệu mục tiêu trực tiếp, bởi vì chúng ta không thấy nhãn cho các ví dụ mà chúng ta thấy trong tự nhiên, trừ khi chúng ta đầu tư vào một đường ống chú thích thời gian thực phức tạp. Tuy nhiên, những gì chúng ta có thể làm là trung bình tất cả các dự đoán mô hình của chúng tôi tại thời điểm thử nghiệm cùng nhau, mang lại đầu ra mô hình trung bình \(\mu(\hat{\mathbf{y}}) \in \mathbb{R}^k\), có \(i^\mathrm{th}\) yếu tố \(\mu(\hat{y}_i)\) là phần nhỏ của tổng dự đoán trên bộ thử nghiệm nơi mô hình của chúng tôi dự đoán \(i\).
Nó chỉ ra rằng trong một số điều kiện nhẹ - nếu bộ phân loại của chúng tôi là chính xác hợp lý ngay từ đầu, và nếu dữ liệu mục tiêu chỉ chứa các danh mục mà chúng ta đã thấy trước đây, và nếu giả định thay đổi nhãn giữ ở nơi đầu tiên (giả định mạnh nhất ở đây), thì chúng ta có thể ước tính nhãn tập kiểm tra phân phối bằng cách giải quyết một hệ thống tuyến tính đơn giản
bởi vì như một ước tính \(\sum_{j=1}^k c_{ij} p(y_j) = \mu(\hat{y}_i)\) giữ cho tất cả \(1 \leq i \leq k\), trong đó \(p(y_j)\) là yếu tố \(j^\mathrm{th}\) của vector phân phối nhãn \(k\) chiều \(p(\mathbf{y})\). Nếu phân loại của chúng tôi đủ chính xác để bắt đầu, thì ma trận nhầm lẫn \(\mathbf{C}\) sẽ có thể đảo ngược và chúng tôi nhận được một giải pháp \(p(\mathbf{y}) = \mathbf{C}^{-1} \mu(\hat{\mathbf{y}})\).
Bởi vì chúng tôi quan sát các nhãn trên dữ liệu nguồn, rất dễ dàng để ước tính phân phối \(q(y)\). Sau đó, đối với bất kỳ ví dụ đào tạo nào \(i\) có nhãn \(y_i\), chúng ta có thể lấy tỷ lệ ước tính của chúng tôi \(p(y_i)/q(y_i)\) để tính trọng lượng \(\beta_i\) và cắm điều này vào giảm thiểu rủi ro thực nghiệm có trọng số trong (4.9.5).
4.9.3.4. Concept Shift Correction¶
Sự thay đổi khái niệm khó khăn hơn nhiều để sửa chữa một cách nguyên tắc. Ví dụ, trong tình huống đột nhiên vấn đề thay đổi từ việc phân biệt mèo với chó sang một trong những phân biệt màu trắng với động vật đen, sẽ không hợp lý khi cho rằng chúng ta có thể làm tốt hơn nhiều so với việc chỉ thu thập nhãn mới và huấn luyện từ đầu. May mắn thay, trong thực tế, những thay đổi cực đoan như vậy là rất hiếm. Thay vào đó, những gì thường xảy ra là nhiệm vụ tiếp tục thay đổi chậm. Để làm cho mọi thứ cụ thể hơn, đây là một số ví dụ:
Trong quảng cáo tính toán, các sản phẩm mới được tung ra, sản phẩm cũ trở nên ít phổ biến hơn. Điều này có nghĩa là việc phân phối trên quảng cáo và mức độ phổ biến của chúng thay đổi dần dần và bất kỳ bộ dự đoán tỷ lệ nhấp qua nào cần phải thay đổi dần dần với nó.
Ống kính camera giao thông suy giảm dần do hao mòn môi trường, ảnh hưởng đến chất lượng hình ảnh dần dần.
Nội dung tin tức thay đổi dần dần (tức là hầu hết các tin tức vẫn không thay đổi nhưng những câu chuyện mới xuất hiện).
Trong những trường hợp như vậy, chúng ta có thể sử dụng cách tiếp cận tương tự mà chúng tôi đã sử dụng cho các mạng đào tạo để làm cho chúng thích ứng với sự thay đổi trong dữ liệu. Nói cách khác, chúng tôi sử dụng trọng lượng mạng hiện có và chỉ cần thực hiện một vài bước cập nhật với dữ liệu mới thay vì đào tạo từ đầu.
4.9.4. Một phân loại của các vấn đề học tập¶
Được trang bị kiến thức về cách đối phó với những thay đổi trong phân phối, giờ đây chúng ta có thể xem xét một số khía cạnh khác của việc xây dựng vấn đề học máy.
4.9.4.1. Học hàng loạt¶
Trong * học theo lô*, chúng tôi có quyền truy cập vào các tính năng đào tạo và nhãn \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\), mà chúng tôi sử dụng để đào tạo một mô hình \(f(\mathbf{x})\). Sau đó, chúng tôi triển khai mô hình này để ghi dữ liệu mới \((\mathbf{x}, y)\) được rút ra từ cùng một phân phối. Đây là giả định mặc định cho bất kỳ vấn đề nào mà chúng tôi thảo luận ở đây. Ví dụ, chúng ta có thể huấn luyện một máy dò mèo dựa trên rất nhiều hình ảnh của mèo và chó. Khi chúng tôi đào tạo nó, chúng tôi vận chuyển nó như một phần của hệ thống thị giác máy tính catdoor thông minh chỉ cho phép mèo vào. Điều này sau đó được cài đặt trong nhà của khách hàng và không bao giờ được cập nhật một lần nữa (cấm hoàn cảnh cực đoan).
4.9.4.2. Học trực tuyến¶
Bây giờ hãy tưởng tượng rằng dữ liệu \((\mathbf{x}_i, y_i)\) đến một mẫu tại một thời điểm. Cụ thể hơn, giả sử rằng lần đầu tiên chúng ta quan sát \(\mathbf{x}_i\), sau đó chúng ta cần phải đưa ra một ước tính \(f(\mathbf{x}_i)\) và chỉ một khi chúng tôi đã làm điều này, chúng tôi quan sát \(y_i\) và với nó, chúng tôi nhận được phần thưởng hoặc phải chịu một sự mất mát, đưa ra quyết định của chúng tôi. Nhiều vấn đề thực sự rơi vào thể loại này. Ví dụ: chúng ta cần dự đoán giá cổ phiếu của ngày mai, điều này cho phép chúng tôi giao dịch dựa trên ước tính đó và vào cuối ngày chúng tôi tìm hiểu xem ước tính của chúng tôi có cho phép chúng tôi kiếm lợi nhuận hay không. Nói cách khác, trong * học trực tuyến*, chúng tôi có chu kỳ sau đây, nơi chúng tôi liên tục cải tiến mô hình của mình cho những quan sát mới.
4.9.4.3. Kẻ cướp¶
Bandits là một trường hợp đặc biệt của vấn đề trên. Trong khi trong hầu hết các vấn đề học tập, chúng ta có hàm tham số liên tục \(f\) nơi chúng ta muốn tìm hiểu các tham số của nó (ví dụ: mạng sâu), trong một vấn đề bandit chúng ta chỉ có một số cánh tay hữu hạn mà chúng ta có thể kéo, tức là, một số hành động hữu hạn mà chúng ta có thể thực hiện. Nó không phải là rất đáng ngạc nhiên rằng đối với vấn đề đơn giản hơn này đảm bảo lý thuyết mạnh mẽ hơn về mặt tối ưu có thể thu được. Chúng tôi liệt kê nó chủ yếu vì vấn đề này thường bị xử lý (gây nhầm lẫn) như thể đó là một bối cảnh học tập riêng biệt.
4.9.4.4. Kiểm soát¶
Trong nhiều trường hợp, môi trường nhớ những gì chúng tôi đã làm. Không nhất thiết phải theo cách đối nghịch nhưng nó sẽ chỉ nhớ và phản ứng sẽ phụ thuộc vào những gì đã xảy ra trước đây. Ví dụ, một bộ điều khiển nồi hơi cà phê sẽ quan sát nhiệt độ khác nhau tùy thuộc vào việc nó đã được sưởi ấm nồi hơi trước đây hay không. Thuật toán điều khiển PID (tỷ lệ tích hợp) là một lựa chọn phổ biến ở đó. Tương tự như vậy, hành vi của người dùng trên một trang tin tức sẽ phụ thuộc vào những gì chúng tôi đã cho anh ta thấy trước đây (ví dụ: anh ta sẽ chỉ đọc hầu hết tin tức một lần). Nhiều thuật toán như vậy tạo thành một mô hình của môi trường mà chúng hành động như để đưa ra quyết định của họ có vẻ ít ngẫu nhiên hơn. Gần đây, lý thuyết điều khiển (ví dụ, các biến thể PID) cũng đã được sử dụng để tự động điều chỉnh các siêu tham số để đạt được chất lượng disentangling và tái thiết tốt hơn, và cải thiện sự đa dạng của văn bản được tạo ra và chất lượng tái thiết của hình ảnh được tạo ra [Shao et al., 2020].
4.9.4.5. Học tăng cường¶
Trong trường hợp chung hơn của một môi trường có bộ nhớ, chúng ta có thể gặp phải các tình huống mà môi trường đang cố gắng hợp tác với chúng tôi (các trò chơi hợp tác, đặc biệt là cho các trò chơi không tổng bằng không) hoặc những người khác nơi môi trường sẽ cố gắng giành chiến thắng. Cờ vua, Go, Backgammon hoặc StarCraft là một số trường hợp trong * tăng cường học về*. Tương tự như vậy, chúng ta có thể muốn xây dựng một bộ điều khiển tốt cho xe ô tô tự trị. Những chiếc xe khác có khả năng đáp ứng với phong cách lái xe tự hành theo những cách không tầm thường, ví dụ, cố gắng tránh nó, cố gắng gây ra tai nạn và cố gắng hợp tác với nó.
4.9.4.6. Xem xét môi trường¶
Một điểm khác biệt chính giữa các tình huống khác nhau ở trên là cùng một chiến lược có thể đã hoạt động trong suốt trường hợp môi trường cố định, có thể không hoạt động trong suốt khi môi trường có thể thích nghi. Ví dụ, một cơ hội chênh lệch giá được phát hiện bởi một nhà giao dịch có khả năng biến mất khi anh ta bắt đầu khai thác nó. Tốc độ và cách thức mà môi trường thay đổi quyết định ở mức độ lớn loại thuật toán mà chúng ta có thể mang lại. Ví dụ, nếu chúng ta biết rằng mọi thứ chỉ có thể thay đổi chậm, chúng ta có thể buộc bất kỳ ước tính nào chỉ thay đổi chậm, quá. Nếu chúng ta biết rằng môi trường có thể thay đổi ngay lập tức, nhưng chỉ rất không thường xuyên, chúng ta có thể làm cho phụ cấp cho điều đó. Những loại kiến thức này rất quan trọng đối với các nhà khoa học dữ liệu tham vọng để đối phó với sự thay đổi khái niệm, tức là, khi vấn đề mà ông đang cố gắng giải quyết những thay đổi theo thời gian.
4.9.5. Công bằng, trách nhiệm giải trình và minh bạch trong học máy¶
Cuối cùng, điều quan trọng cần nhớ là khi bạn triển khai các hệ thống machine learning, bạn không chỉ đơn thuần là tối ưu hóa một mô hình dự đoán — bạn thường cung cấp một công cụ sẽ được sử dụng để tự động hóa các quyết định (một phần hoặc toàn bộ). Các hệ thống kỹ thuật này có thể ảnh hưởng đến cuộc sống của các cá nhân phải chịu các quyết định kết quả. Bước nhảy vọt từ việc xem xét các dự đoán cho các quyết định đặt ra không chỉ các câu hỏi kỹ thuật mới, mà còn là một loạt các câu hỏi đạo đức phải được xem xét cẩn thận. Nếu chúng ta đang triển khai một hệ thống chẩn đoán y tế, chúng ta cần biết quần thể nào nó có thể hoạt động và nó có thể không. Nhìn ra những rủi ro có thể thấy trước đối với phúc lợi của một nhóm dân số có thể khiến chúng ta phải chăm sóc kém hơn. Hơn nữa, một khi chúng ta chiêm ngưỡng các hệ thống ra quyết định, chúng ta phải lùi lại và xem xét lại cách chúng ta đánh giá công nghệ của mình. Trong số các hậu quả khác của sự thay đổi phạm vi này, chúng tôi sẽ thấy rằng độ chính xác hiếm khi là biện pháp phù hợp. Ví dụ, khi dịch dự đoán thành hành động, chúng ta thường sẽ muốn tính đến độ nhạy chi phí tiềm năng của việc sai phạm theo nhiều cách khác nhau. Nếu một cách phân loại sai hình ảnh có thể được coi là một sự buồn ngủ về chủng tộc, trong khi việc phân loại sai cho một danh mục khác sẽ vô hại, thì chúng ta có thể muốn điều chỉnh ngưỡng của mình cho phù hợp, chiếm các giá trị xã hội trong việc thiết kế giao thức ra quyết định. Chúng tôi cũng muốn cẩn thận về cách các hệ thống dự đoán có thể dẫn đến các vòng phản hồi. Ví dụ, xem xét các hệ thống chính sách dự đoán, phân bổ các sĩ quan tuần tra cho các khu vực có tội phạm dự báo cao. Thật dễ dàng để thấy một mô hình đáng lo ngại có thể xuất hiện như thế nào:
Các khu phố có nhiều tội phạm hơn nhận được nhiều tuần tra hơn.
Do đó, nhiều tội ác được phát hiện ở các khu phố này, nhập dữ liệu đào tạo có sẵn cho các lần lặp lại trong tương lai.
Tiếp xúc với những tích cực hơn, mô hình dự đoán nhiều tội phạm hơn ở những khu phố này.
Trong lần lặp tiếp theo, mô hình được cập nhật nhắm vào cùng một khu phố thậm chí còn nhiều hơn dẫn đến nhiều tội ác hơn được phát hiện, v.v.
Thông thường, các cơ chế khác nhau mà các dự đoán của một mô hình trở nên kết hợp với dữ liệu đào tạo của nó không được tính đến trong quá trình mô hình hóa. Điều này có thể dẫn đến những gì các nhà nghiên cứu gọi là * vòng lặp phản hồi runaway*. Ngoài ra, chúng tôi muốn cẩn thận về việc liệu chúng tôi có đang giải quyết đúng vấn đề ngay từ đầu hay không. Các thuật toán tiên đoán bây giờ đóng một vai trò lớn hơn trong việc trung gian việc phổ biến thông tin. Có nên tin tức rằng một cuộc gặp gỡ cá nhân được xác định bởi tập hợp các trang Facebook mà họ có *Liked* không? Đây chỉ là một vài trong số nhiều tình huống khó xử đạo đức cấp bách mà bạn có thể gặp phải trong sự nghiệp học máy.
4.9.6. Tóm tắt¶
Trong nhiều trường hợp đào tạo và bộ thử nghiệm không đến từ cùng một phân phối. Đây được gọi là dịch chuyển phân phối.
Rủi ro là kỳ vọng về sự mất mát đối với toàn bộ dân số dữ liệu được rút ra từ phân phối thực sự của họ. Tuy nhiên, toàn bộ dân số này thường không có sẵn. Rủi ro thực nghiệm là một tổn thất trung bình so với dữ liệu đào tạo để gần đúng rủi ro. Trong thực tế, chúng tôi thực hiện giảm thiểu rủi ro thực nghiệm.
Theo các giả định tương ứng, covariate và thay đổi nhãn có thể được phát hiện và sửa chữa tại thời điểm thử nghiệm. Việc không tính đến sự thiên vị này có thể trở nên có vấn đề tại thời điểm thử nghiệm.
Trong một số trường hợp, môi trường có thể nhớ các hành động tự động và phản ứng theo những cách đáng ngạc nhiên. Chúng ta phải tính đến khả năng này khi xây dựng các mô hình và tiếp tục giám sát các hệ thống trực tiếp, mở ra khả năng các mô hình và môi trường của chúng tôi sẽ bị vướng vào những cách không lường trước.
4.9.7. Bài tập¶
Điều gì có thể xảy ra khi chúng ta thay đổi hành vi của một công cụ tìm kiếm? Người dùng có thể làm gì? Còn các nhà quảng cáo thì sao?
Thực hiện một máy dò thay đổi covariate. Gợi ý: xây dựng một phân loại.
Thực hiện một corrector thay đổi covariate.
Bên cạnh sự thay đổi phân phối, điều gì khác có thể ảnh hưởng đến rủi ro thực nghiệm gần đúng rủi ro như thế nào?
